Kaggle time series data – An easy introduction
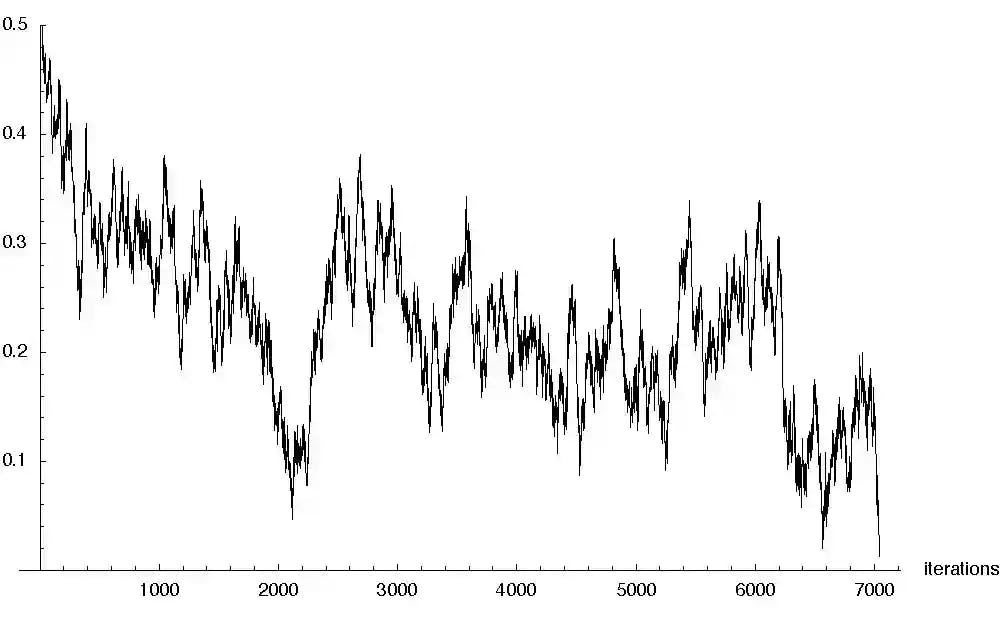
A time series is a collection of observations on at least one variable ordered along single dimension, time. A time series data demonstrates properties such as large data size, abundant attributes and continuity. Time series forecasting is particularly useful in an analysis of a trend and forecasting in macroeconomics. In the field of finance time series data assists in forecasting volatility and an average price.

Kaggle Time Series Data Examples
Time series data examples include the broad macroeconomic aggregates such as price levels, money supply, exchange rates, gross domestic product, investments, relative income levels and productivity indicators. Stock prices and cryptocurrency prices are also instances of time series data. For instance, you can find Bitcoin historical price 1-minute data from 2012 to 2021 on Kaggle.
Time Dependence
The key feature of time series data is time dependence. The data points tend to exhibit strong relationship to their recent histories, lags. This feature creates a critical problem in utilizing time series data in a standard econometric model. Researchers need to take additional steps in specifying econometric models for time series data before using them in standard econometric methods.
The emphasis in econometrics of time series is the dependence among observations at multiple points in time. In addition to the highly correlated temporal order among different variables, relationships between their current and past values are critical.
Time series forecasting
Furthermore, an appropriate forecasting model can be constructed to capture the dynamics of the underlying time series, which can provide a basis for investors’ decision-making. For example, an accurate forecasting of the stock index allows investors to grasp the overall trend of the market to effectively capture trading opportunity and make reasonable asset allocations.
The classical forecasting models of time series are auto-regressive model (AR), moving-average model (MA), auto-regressive moving average model (ARMA) and auto-regressive integrated moving average model (ARIMA). In turn, the ARIMA model has become one of the more widely used methods in the study of forecasting models for time series.
Stock index time series forecasting in Python
To illustrate operations with time series data in python we use 6 years of 5 minute NIFTY 50 Indian stock index data set from Kaggle. The data spans from 9 January 2015 to 25 March 2021.
First, we import necessary libraries and install new one in Kaggle environment:
import numpy as np
import pandas as pd
from statsmodels.graphics.tsaplots import plot_pacf, plot_acf
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.ar_model import AR
!pip install arch >/dev/null
from arch.univariate import ARX, ARCH, GARCH
import warnings
warnings.filterwarnings('ignore')
pd.set_option('display.max_rows', 1000)
We also load the data set using pandas library read_csv() method. We process the date column with Datetime library strptime() method to a datetime data type compatible with Pandas DataFrame.
def parser(s):
return datetime.strptime(s[:19], '%Y-%m-%d %H:%M:%S')
df = pd.read_csv("/kaggle/input/6-year-nifty50-historical-data-of-5-30-min-candle/5min_N50_10yr.csv", usecols = ['date','close'], parse_dates=['date'], date_parser=parser, index_col='date')
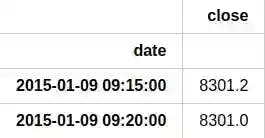
The pandas methodhead(2) displays first 2 rows of the data, meanwhile info() dispays information about the tpyes of the columns and DataFrame properties. We also set date column as an index:
df.head(2)
df.info()

Visualization
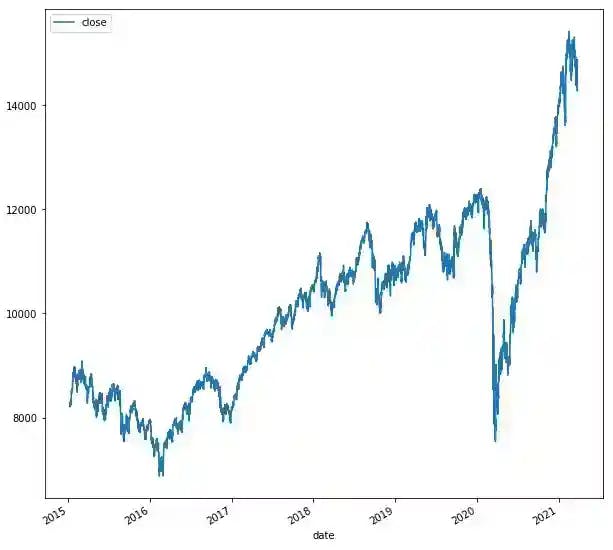
The stock price index data chart looks as following:
df.plot(figsize=(10,10))
plt.savefig('plot.png')# to save the plot
plt.show()
Moreover, we can plot the data set and conduct a time series analysis using partial auto-correlation and auto-correlation plots that we will cover in details in the future:
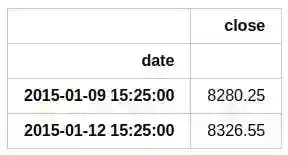
But first we save only daily stock close values to conduct daily stock price analysis. To conduct a higher frequency analysis we need tan access to more granular data from markets across the world.
data = df[(df.index.minute==25)&(df.index.hour==15)]
data.head(2)
Autocorrelation plots
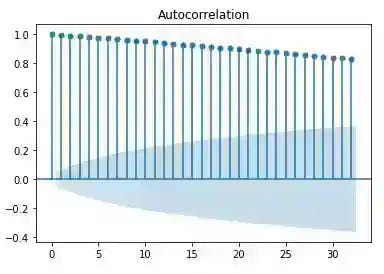
For plotting auto-correlations we use statsmodels library. Here is an example of autocorrelation and partial autocorrelation plots for stock index price data.
plot_acf(data['close'])
plt.savefig('acf.png')
plt.show()
plot_pacf(data['close'])
plt.savefig('pacf.png')
plt.show()
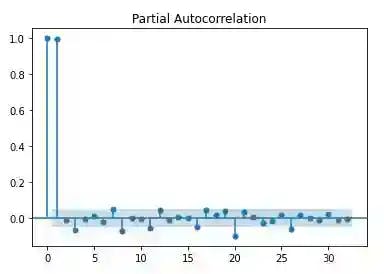
Clearly there is evidence for time-dependence and serial correlation. Hence, we should convert the prices to a log-price due to the property of symmetry around zero and difference the data for stationarity.
def log_return(list_stock_prices):
return np.log(list_stock_prices).diff()
data['log_return'] = log_return(data.close)
We visualize the time series plot of log-price with matplotlib:
data.log_return.plot(figsize=(10,10))
plt.savefig('log.png')
plt.show()
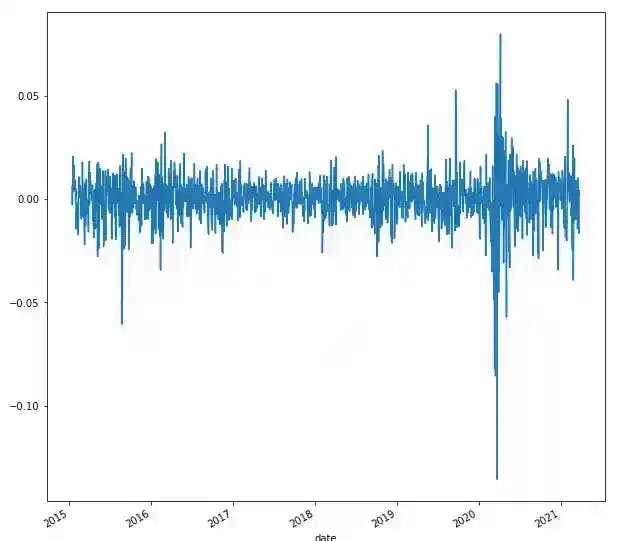
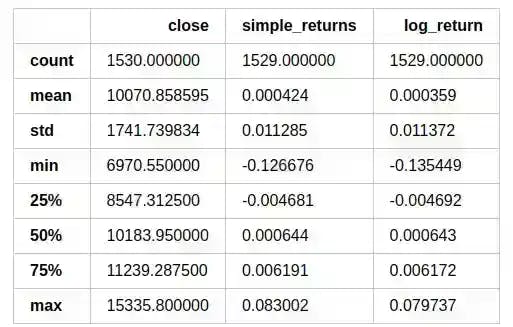
We also provide comparative descriptive statistics. In a normal distribution mean equals median.
data.describe()
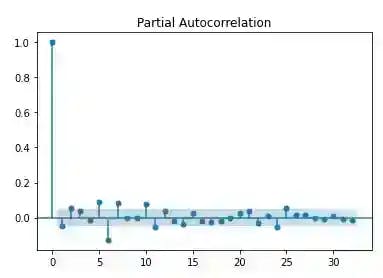
plot_pacf(data['log_return'].dropna())
plt.savefig('dacf.png')
plt.show()
plot_acf(data['log_return'].dropna())
plt.savefig('dpacf.png')
plt.show()
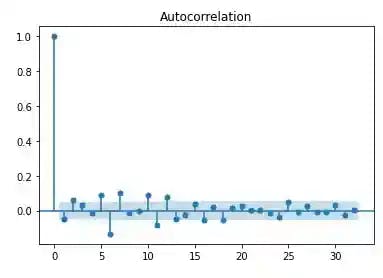
The plot of differenced log-returns exhibits a constant mean, variance and auto-correlation function.
You can access the data and code on Kaggle.
Related Posts
- How to Panel data python – An easy introduction
- Blockchain Data Indexer with TrueBlocks
- Advanced Realized Volatility and Quarticity
- Machine Learning with Simple Sklearn Ensemble
- Parsiq Triggers for Axie Infinity
- How to illustrate log returns vs simple returns
- A How to EfficientNet Classification
- Unlock the Power of Decentralization with PinSave